Crop mapping with satellite data¶
Benson Kenduiywo
Background¶
Mapping the distribution of crops is important for several applications. A problem with using remote sensing data for crop mapping is the presence of clouds. As crops are typically grown in the rainy seasons, they may be difficult to detect with the commonly used optical reflectance data. Radar remote sensing data is not affected by weather conditions (or the presence of daylight), and that makes it a very interesting alternative to optical data. Here we use Sentinel-1 radar data to map different crop types in Kitale, Kenya. We build on the approaches introduced in the introduction to remote sensing tutorial, but we focus on other aspects (feature creation and model evaluation).
Data¶
We provide a set of processed Sentinel-1 VV and VH polarized images. To learn about the basics of radar visit EO College, SERVIR SAR HANDBOOK or European Space Agency (ESA) tutorials. The images are ground range products with equidistant pixel spacing. They were radiometrically calibrated to \(\sigma_0\). All images were co-registered and transformed to the UTM-36N and WGS1984 datum coordinate reference system.
Here is how you can get the Sentinel data for this tutorial.
workdir <- file.path(dirname(tempdir()))
datadir <- file.path(workdir, "reagro/sentinel")
dir.create(datadir, showWarnings=FALSE, recursive=TRUE)
Get the ground observations. We download the data with the “agrodata” package.
ff <- agrodata::data_crop("sentinel", datadir)
head(ff)
## [1] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VH_2015_09_15_Clip.tif"
## [2] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VH_2015_12_20_Clip.tif"
## [3] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VV_2015_03_07_Clip.tif"
## [4] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VV_2015_03_31_Clip.tif"
## [5] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VV_2015_05_18_Clip.tif"
## [6] "c:/temp/reagro/sentinel/S1A_IW_A_GRDH_VV_2015_06_11_Clip.tif"
Here is just a trick to skip some preprocessing if that has already been done
imgfile <- file.path(workdir, "img.tif")
imgexists <- file.exists(imgfile)
You can use the grep funtion to get the VV polarized images.
fvv <- grep("VV", ff, value = TRUE)
i <- order(substr(basename(fvv), 15, 27))
fvv <- fvv[i]
head(basename(fvv))
## [1] "S1A_IW_A_GRDH_VV_2015_03_07_Clip.tif"
## [2] "S1A_IW_D_GRDH_VV_2015_03_14_Clip.tif"
## [3] "S1A_IW_D_GRDH_VV_2015_03_21_Clip.tif"
## [4] "S1A_IW_A_GRDH_VV_2015_03_31_Clip.tif"
## [5] "S1A_IW_D_GRDH_VV_2015_04_07_Clip.tif"
## [6] "S1A_IW_D_GRDH_VV_2015_04_14_Clip.tif"
Now create a SpatRaster object
library(terra)
vv <- rast(fvv)
# make prettier (shorter) layer names
names(vv) <- substr(names(vv), 15, 27)
names(vv)
## [1] "VV_2015_03_07" "VV_2015_03_14" "VV_2015_03_21" "VV_2015_03_31"
## [5] "VV_2015_04_07" "VV_2015_04_14" "VV_2015_05_01" "VV_2015_05_18"
## [9] "VV_2015_06_01" "VV_2015_06_11" "VV_2015_06_25" "VV_2015_07_05"
## [13] "VV_2015_07_12" "VV_2015_07_19" "VV_2015_07_29" "VV_2015_08_22"
## [17] "VV_2015_08_29" "VV_2015_09_15" "VV_2015_10_09" "VV_2015_10_16"
## [21] "VV_2015_11_02" "VV_2015_11_09" "VV_2015_11_16" "VV_2015_11_26"
## [25] "VV_2015_12_10" "VV_2015_12_20"
vv
## class : SpatRaster
## dimensions : 982, 783, 26 (nrow, ncol, nlyr)
## resolution : 10, 10 (x, y)
## extent : 705883.3, 713713.3, 112681.4, 122501.4 (xmin, xmax, ymin, ymax)
## coord. ref. : WGS 84 / UTM zone 36N (EPSG:32636)
## sources : S1A_IW_A_GRDH_VV_2015_03_07_Clip.tif
## S1A_IW_D_GRDH_VV_2015_03_14_Clip.tif
## S1A_IW_D_GRDH_VV_2015_03_21_Clip.tif
## ... and 23 more source(s)
## names : VV_20~03_07, VV_20~03_14, VV_20~03_21, VV_20~03_31, VV_20~04_07, VV_20~04_14, ...
## min values : -23.63815, -24.24532, -23.842509, -24.12050, -21.34933, -22.599835, ...
## max values : 11.09030, 18.05906, 8.262378, 12.79875, 20.11449, 7.086701, ...
Repeat the steps for vh polarization.
fvh <- grep("VH", ff, value = TRUE)
i <- order(substr(basename(fvh), 15, 27))
fvh <- fvh[i]
vh <- rast(fvh)
names(vh) <- substr(names(vh), 15, 27)
names(vh)
## [1] "VH_2015_04_07" "VH_2015_09_15" "VH_2015_12_20"
We also have ground reference data on crop types.
cropref <- agrodata::data_crop("crop_ref")
head(cropref)
## x y class
## 1 711908.3 117516.4 Maize
## 2 710608.3 113696.4 Maize
## 3 712178.3 116916.4 Maize
## 4 711978.3 120526.4 Maize
## 5 710858.3 115086.4 Maize
## 6 711068.3 119616.4 Maize
table(cropref$class)
##
## Grass Maize Pasture Wheat
## 500 500 500 500
Create a SpatVector object
vecref <- vect(cropref, geom=c("x", "y"), crs=crs(vv))
vecref
## class : SpatVector
## geometry : points
## dimensions : 2000, 1 (geometries, attributes)
## extent : 705928.3, 713278.3, 112916.4, 122286.4 (xmin, xmax, ymin, ymax)
## coord. ref. : WGS 84 / UTM zone 36N (EPSG:32636)
## names : class
## type : <chr>
## values : Maize
## Maize
## Maize
plot(vecref, "class", plg=list(x="bottomleft"))
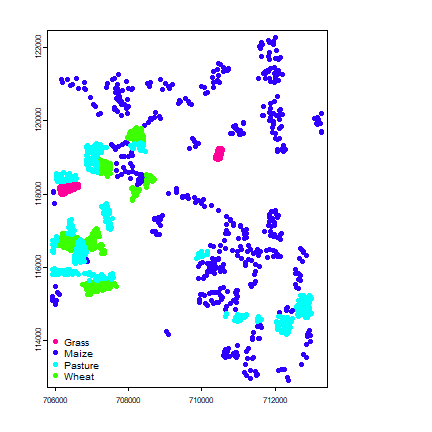
As you can see, the points were generated by sampling within fields.
Feature creation¶
We have “raw” time series satellite data, and many more images for VV than for VH. We can use these data to build a model to predict crop types, but oftentimes we prefer to compute new “features” (predictor variables) from the raw data. These new features should typically reduce the number of variables (images), while capturing perhaps more of the variation in the data.
Here is a function to compute features. It takes a multi-layer
SpatRaster x to create new layers.
compFeatures <- function(x, name){
# standard deviation
stdev <- stdev(x)
# quantiles
quant <- app(x, function(i) quantile(i, c(.1, .25, .5, .75, .9)))
# trend
n <- nlyr(x)
trend <- 100 * (mean(x[[1:5]] - mean(x[[(n-4):n]])))
feat <- c(quant, stdev, trend)
names(feat) <- paste0(name, c(".1", ".25", ".5", ".75", ".9", ".sd", "trend"))
return(feat)
}
Compute seasonal composite features from VV polarized images
fvv <- file.path(workdir, "vv_ft.tif")
if (!file.exists(fvv)) {
vv_ft <- compFeatures(vv, "vv")
writeRaster(vv_ft, fvv)
} else {
vv_ft <- rast(fvv)
}
vv_ft
## class : SpatRaster
## dimensions : 982, 783, 7 (nrow, ncol, nlyr)
## resolution : 10, 10 (x, y)
## extent : 705883.3, 713713.3, 112681.4, 122501.4 (xmin, xmax, ymin, ymax)
## coord. ref. : WGS 84 / UTM zone 36N (EPSG:32636)
## source : vv_ft.tif
## names : vv.1, vv.25, vv.5, vv.75, vv.9, vv.sd, ...
## min values : -22.198498, -21.384859, -20.158096, -19.26714, -18.70032, 0.781612, ...
## max values : -4.023386, -2.551054, 2.724735, 12.20475, 19.68188, 13.250704, ...
plot(vv_ft[[1:4]])
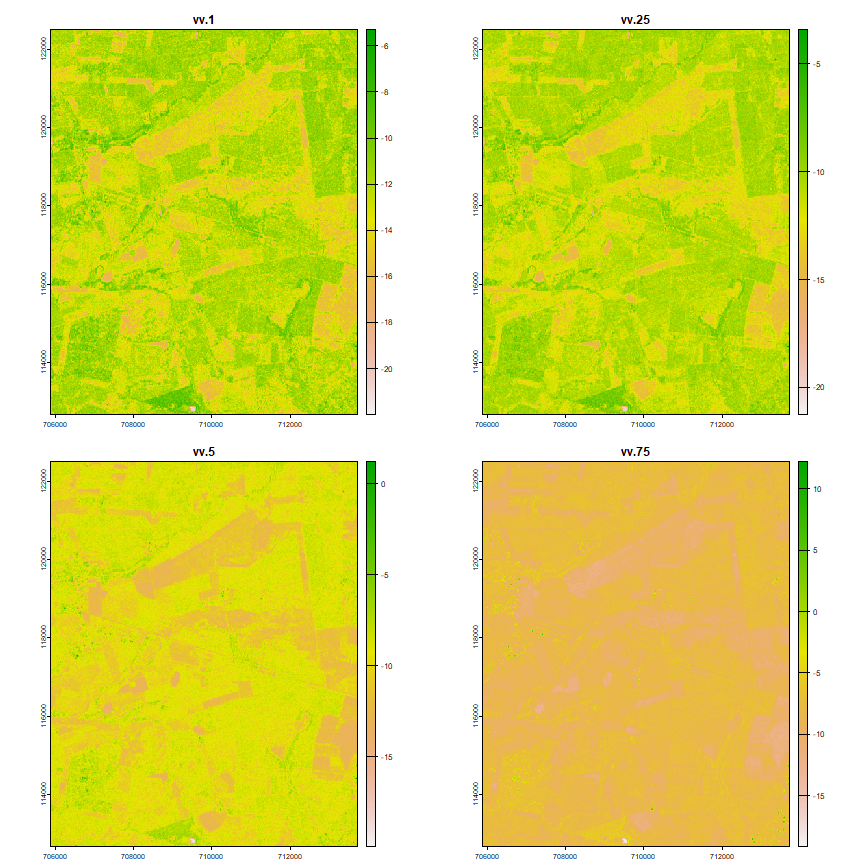
As we only have four images for VH polarized images, we cannot use the function above to create features, we’ll just use the mean and the standard deviation.
fvh <- file.path(workdir, "vh_ft.tif")
if (!file.exists(fvh)) {
sd <- stdev(vh)
mn <- mean(vh)
vh_ft <- c(mn, sd)
names(vh_ft) <- c("mean", "stdev")
writeRaster(vh_ft, fvh)
} else {
vh_ft <- rast(fvh)
}
plot(vh_ft)
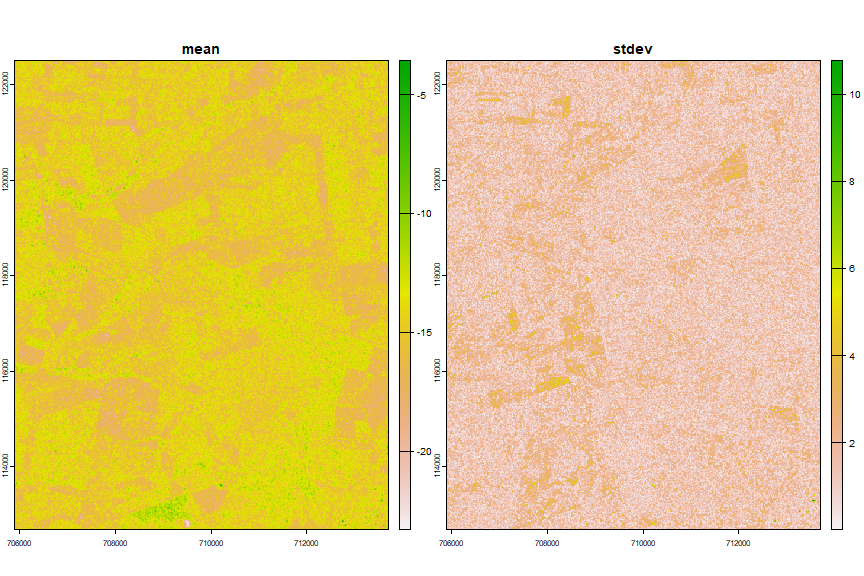
Combine the vv and vh features
img <- c(vv_ft, vh_ft)
Model fitting¶
Various supervised classification algorithms exist, and the choice of algorithm affects the results. Here we used the widely used Random Forests (RF) alogirthm (Breiman 2001).
Random Forests makes predictions using an ensemble of a large number of decision trees. The individual trees are uncorrelated because they are fitted with different subsets of the data. Each tree is fitted with a bootstrapped sample of all the data. A bootstrapped sample is obtained by taking a sample with replacement of the same size as the original data. RandomForest also uses a maximum user-defined number of variables that can randomly selected from to create a node. A different sample is used at each node. Thus each tree has a somewhat different data set and the “best” variable is not always avaiable to create a node. The final prediction (by the forest) is made by averaging the prediction of the individual trees.
The user needs to set the number of trees to build. The more trees, the longer it takes to build the model and to make predictions. Generally, RandomForests models tend to be stable once there are 200 trees (Hastie et al. (2009)).
To train a model, we extract the satellite data for the ground points, using the feature (predictor) data created above.
ref <- extract(img, vecref, drop=TRUE)
ref <- data.frame(class=cropref$class, ref[,-1])
ref$class <- as.factor(ref$class)
head(ref)
## class vv.1 vv.25 vv.5 vv.75 vv.9 vv.sd
## 1 Maize -11.05758 -10.481299 -8.789228 -7.538952 -6.349695 1.914231
## 2 Maize -15.24834 -11.633831 -9.693624 -8.460844 -6.773844 3.118843
## 3 Maize -11.99607 -9.939957 -9.011965 -7.437552 -6.433441 2.174761
## 4 Maize -12.43187 -10.576469 -8.890006 -7.028844 -6.291332 2.285031
## 5 Maize -11.04900 -9.541140 -8.504607 -7.691144 -6.656007 1.935807
## 6 Maize -12.99435 -11.343201 -9.721516 -8.689487 -7.166204 2.183923
## vvtrend mean stdev
## 1 0.3630066 -14.67873 1.0157369
## 2 -354.3470764 -13.42899 1.1117842
## 3 -66.2557907 -14.25952 0.8469766
## 4 -166.5378876 -13.62759 3.1410534
## 5 22.8595829 -16.61568 0.9409202
## 6 -181.8577728 -14.84602 1.2008991
Now we can train the model
library(randomForest)
## randomForest 4.7-1.1
## Type rfNews() to see new features/changes/bug fixes.
set.seed(888)
rf.m <- randomForest(class~., data=ref, ntree=250, importance=TRUE)
When we print the model object, we get some diagnostics. Can you understand them? What does “OOB” mean?
rf.m
##
## Call:
## randomForest(formula = class ~ ., data = ref, ntree = 250, importance = TRUE)
## Type of random forest: classification
## Number of trees: 250
## No. of variables tried at each split: 3
##
## OOB estimate of error rate: 33.15%
## Confusion matrix:
## Grass Maize Pasture Wheat class.error
## Grass 346 35 62 57 0.308
## Maize 39 397 18 46 0.206
## Pasture 84 40 316 60 0.368
## Wheat 83 55 84 278 0.444
We can also plot the model object
cols <- c("green", "yellow", "darkgreen", "magenta", "blue")
plot(rf.m, col=cols, lwd=3)
legend("topright", col=cols , c("OOB", "Grass", "Maize","Pasture","Wheat"), lty=1, lwd=3)
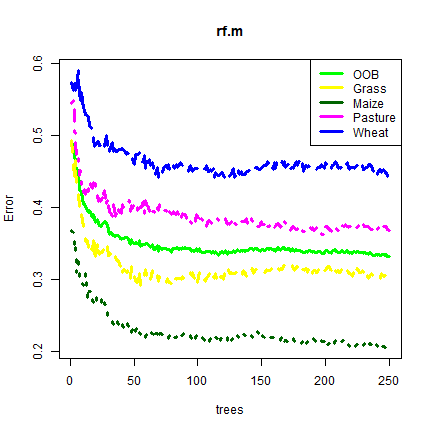
There is a number of other tools to inspect the model. The “Variable Importance Plot” is an important tool that can be used with any regression-like model to determine the importance of individual variables.
varImpPlot(rf.m, main="")
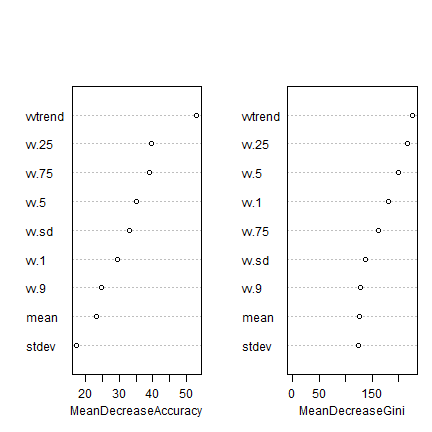
The plot shows each variable on the y-axis, and their importance on the x-axis. They are ordered top-to-bottom as most- to least-important. There are two plots namely:
Mean decrease in accuracy. The lower the predictive performance of Random Forest due to the exclusion (randomization of the values, in fact) of particular single variable, the more important the variable is.
Mean decrease in Gini estimates the contribution of each variable to achieve homogeneity in the groups created by the trees. Every time a variable is used to split the data (create a node), the Gini coefficient for the child nodes are estimated and compared to that of the data of the mother node. The Gini coefficient is a measure of homogeneity in the range of 0 (homogeneous) to 1 (heterogeneous). Variables that result in nodes with higher purity have a higher decrease in Gini coefficient.
You can also look at the raw data used to make the plot
importance(rf.m)
## Grass Maize Pasture Wheat MeanDecreaseAccuracy
## vv.1 10.105986 16.1734497 27.4282308 5.443300 29.43520
## vv.25 14.044807 28.0127391 29.9908397 8.211039 39.49790
## vv.5 8.822775 27.0401383 22.4889809 11.388447 35.04791
## vv.75 14.494611 30.0929148 12.3366393 8.640554 39.10032
## vv.9 16.304916 18.3853564 8.2060896 3.908597 24.60054
## vv.sd 25.061318 13.5025359 16.9865510 5.653507 33.09875
## vvtrend 29.433321 9.8514908 27.7145533 40.925422 53.12528
## mean 19.761603 -1.5814918 10.1693232 14.423917 23.16764
## stdev 16.650163 -0.0134983 0.5681341 13.370582 17.27973
## MeanDecreaseGini
## vv.1 179.9310
## vv.25 217.0500
## vv.5 199.7379
## vv.75 161.1420
## vv.9 127.2613
## vv.sd 137.7662
## vvtrend 226.1858
## mean 126.5551
## stdev 123.6140
Another good diagnostic tool is the partial-plot. It shows the response to a single variable (all other variables are kept at their original values).
partialPlot(rf.m, ref, "vvtrend", "Maize")
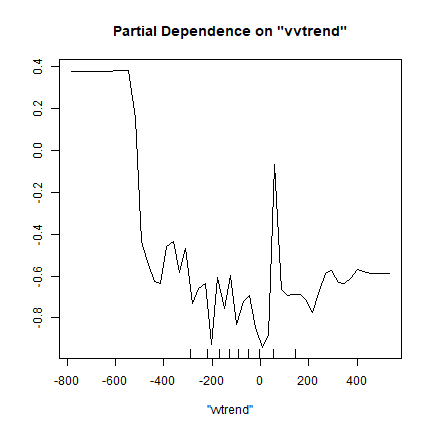
Like the variable importance plot, the partial plot can be computed for any regression-like (or classification) model; but there is not always a simple function available to quickly do it.
Model prediction¶
Now we use the model to predict the distribution of crops over the entire study region. This is the easy part.
rf.pred <- predict(img, rf.m)
rf.pred
## class : SpatRaster
## dimensions : 982, 783, 1 (nrow, ncol, nlyr)
## resolution : 10, 10 (x, y)
## extent : 705883.3, 713713.3, 112681.4, 122501.4 (xmin, xmax, ymin, ymax)
## coord. ref. : WGS 84 / UTM zone 36N (EPSG:32636)
## source(s) : memory
## categories : class
## name : class
## min value : Grass
## max value : Wheat
Make a map
levels(rf.pred) <- data.frame(ID=1:4, class=c("Grassland", "Maize", "Pasture", "Wheat"))
plot(rf.pred, col=c("green", "yellow", "darkgreen", "magenta"))
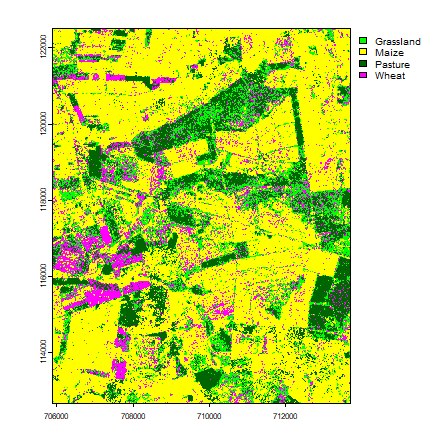
Post classifation improvements¶
TO DO: show and discuss the removal of noise
Model evaluation¶
It is important to evaluate predictive models. It allows comparison with alternative methods, and it can help establish some confidense in the predictions. Predictive models are generally evaluated with “cross-validation”. This is a technique in which the data are split in k folds. Each fold is held out once to evaluate the model created with the other folds. An evaluation statistic is computed for each fold, and averaged. Typically we use 5 or 10 fold cross-validation (do not use more folds).
Let’s make 5 “folds”. That is, each record is assinged to one of 5 groups
library(predicts)
set.seed(530)
k <- sample(5, nrow(ref), replace=TRUE)
nrow(ref) / 5
## [1] 400
table(k)
## k
## 1 2 3 4 5
## 395 386 413 406 400
We now would need a loop to go over each fold, but here we just show the approach for a single fold.
Get training and testing samples
train <- ref[k != 1, ]
test <- ref[k == 1, ]
Build a new model
rf <- randomForest(class~., data=train, ntree=250, importance=TRUE)
And use the model to make a prediction for the test data. Importantly, the model did not see the test data!
pred <- predict(rf, test)
And create a confusion matrix
conmat <- table(observed=test$class, predicted=pred)
conmat
## predicted
## observed Grass Maize Pasture Wheat
## Grass 65 7 15 8
## Maize 12 66 2 13
## Pasture 13 13 63 23
## Wheat 17 4 18 56
Compute one or more statistics
library(luna)
# overall accuracy
evaluate(conmat, "overall")
## [1] 0.6329114
# kappa
evaluate(conmat, "kappa")
## [1] 0.5105287
# user and producer accuracy
evaluate(conmat, "class")
## Grass Maize Pasture Wheat
## row-wise 0.6842105 0.7096774 0.5625000 0.5894737
## col-wise 0.6074766 0.7333333 0.6428571 0.5600000
References¶
Breiman, L., 2001. Random forests. Machine learning, 45(1), 5-32.
James, G., D. Witten, T. Hastie and R. Tibshirani, 2013. An Introduction to Statistical Learning. Springer.